Temporal Data Skeletons

La représentation du temps dans les données et ses modes de contrôle via des interfaces constituent un champ toujours fertile d’invention dans le domaine de l’analyse des données. L’intérêt pour ce domaine des data sciences redouble ces derniers temps dans le sillage des problématiques de contrôle des données massives, temps réel, en réseau et le plus souvent multi-sources. La plupart des solutions développées jusqu’à aujourd’hui, à titre de projet d’interface expérimentale comme d’interfaces opérationnelles, épousent le principe d’une représentation axiale du «temps» ou des time-series présentes dans les bases de données. On considère ainsi souvent le temps comme un vecteur qui contraint l’espace de l’interface, de la dynamique d’un objet particulier aux évolutions globales de structures.

C’est le cas dans le domaine des réseaux et des graphes où les solutions adoptées sont basées sur la notion d’axe temporel: à partir d’une time-line on peut rétrospectivement visualiser l’évolution d’une structure complexe (information IN the net: apparition/disparition des nœuds et de liens en fonction de paliers temporels) ou la dynamique des flux et des phénomènes de propagation sur une structure (information ON the net, circulation d’une information ou de tout autre élément sur la structure de graphe. La time-line de Gephi permet par exemple de faire défiler cinématographiquement les configurations topologiques d’une structure complexe (avance, retour, pose, lecture, réglage de la fenêtre temporelle…). Au-delà du champ de la visualisation des graphes, on retrouve le même principe d’axialisation dans de  nombreux projets  en infovis ou en design d’interfaces où le temps distribue les objets dans un espace alors vectorisé (de gauche à droite, de haut en bas, de façon circulaire, en spirale dans un univers 3D, de façon circulaire…).

Cependant, dans le domaine des graphes ou peut-être au-delà en infovis, que l’on adopte une solution de type graph streaming (par exemple Gephi avec sa time line) ou une solution de type frise chronologique, ces représentations axiales nourrissent l’idée que le « temps » serait en quelque sorte «extérieur aux données», comme un cadre abstrait et étranger au monde des formes sensibles, peut-être même une dimension spécifique (la fameuse 4^e dimension de l’espace euclidien). Or, il est toujours possible dans une approche par graphe de traiter les séries temporelles comme un ordonnancement chronologique déformable, autrement dit d’inscrire la succession des événements (dotés d’un indicateur chronologique: année, mois, jour, minute…) sous la forme a) d’une chaîne ou d’une ligne temporelle de nœuds reliés entre eux (un squelette chronologique constitué d’événements) b) elle-même reliée à une autre dimension de l’information ou d’un autre attribut (par exemple des acteurs, des descripteurs, des mots-clés…). En termes plus techniques il s’agit de produire un graphe bipartite constitué de nœuds «événements» consécutifs reliés entre eux de façon linéaire (éventuellement en attribuant aux liens des jeux de force) et simultanément reliés à une autre dimension d’un jeu de données (par exemple des acteurs ayant participé à un ou plusieurs événements).

Dans le domaine des graphes appliqués à l’analyse de données, on peut ainsi visuellement synthétiser des milliers d’actions (par exemple les connexions-serveur, likes, tweets, emails, chats…) réalisées par un acteur connecté avec son entourage ou même plusieurs acteurs interagissant entre eux. Ce procédé permet d’imprimer à l’axe du temps (le squelette temporel constitué d’événements reliés entre eux) des déformations significatives de trajectoires individuelles ou collectives dans un ou plusieurs espaces d’interaction en ligne comme les réseaux sociaux et les outils de communication mobiles. Le principe semble constituer une piste d’expérimentation intéressante pour concentrer dans une interface une solution d’observation ou de contrôle des données pour des systèmes d’informations multi-sources, multi-utilisateurs et temps réel.

1. Méthode

La méthode adoptée s’inscrit dans l’univers de la spatialisation de graphes à base d’algorithmes de type force-directed, en particulier tels qu’ils sont développés dans la culture technologique autour de Gephi et de ses communautés (utilisateurs individuels, start-ups comme linkurio.us, linkfluence, Atelier Iceberg, E–minove). Elle repose sur le principe d’une déformation significative d’un axe du temps rendu présent dans le graphe (et non sous forme d’une time-line extérieure aux données). Techniquement, l’approche à base de graphes peut reposer sur le croisement de deux colonnes d’une table de données (par exemple des auteurs et des publications), les time-series étant mobilisées de façon annexe pour faire évoluer la structure bi-partite (auteurs et publications selon les années). La méthode testée dans nos expérimentations repose sur l’idée d’introduire dans le graphe des événements successifs (éventuellement associés à des formes de datation : année/mois/jours/minutes/secondes…) reliés entre eux via des liens de consécution. Avec l’algorithme ForceAtlas2, on obtient une droite que l’on peut ensuite déformer en introduisant une seconde famille de nœuds, par exemple des acteurs ayant participé aux événements. Le principe peut être testé aisément sous Gephi: l’introduction successive d’acteurs (en rouge) reliés à des événements (en noir) produit des effets de déformation de la structure linéaire:

Au final, le graphe bi-partite (événements/acteurs) se transforme en graphe «classique» où sont mises en valeur les qualités structurales habituelles des spatialisations avec les algorithmes ForceAtlas1 et 2: effets de concentration et de périphérie, apparition de clusters et de propriétés topologiques calculables comme les distances (proximité/éloignement, centre/périphérie, densité…). Cette transformation progressive conduit à deux difficultés majeures: la première, et la plus évidente, est que l’on perd littéralement le principe de succession temporelle ou de parcours dynamique. La seconde, directement associée, est liée au nombre de données traitables: passés certains seuils quantitatifs (au-delà d’une centaine de nœuds et de quelques centaines de liens), la spatialisation débouche sur le fameux « plat de spaghetti », irréductible à priori pour de nombreux usagers. Dans une première expérimentation, un graphe d’un milliers de SMS échangés ont été extraits d’un compte personnel via smsTocsv sous Androïd. Il s’agit du graphe des échanges d’un étudiant de l’U.T.C. sur une période de plus de deux années et dans l’environnement social d’une école d’ingénieur où les contacts d’un étudiant font souvent apparaître un nombre réduit et central de correspondants (membres de la famille et amis personnels) que l’on supposer relativement stable dans le temps. Avec 1062 nœuds (nœuds de chacun des SMS regroupés par jour de l’année + nœuds des correspondants) et 5254 liens, le graphe spatialisé en ForceAtlas2 fait apparaître un phénomène d’affaissement où les données sont concentrées dans un cœur extrêmement dense visuellement (statistiquement, la densité structurale est plutôt faible).

Pour pallier à cet effet de concentration, on peut pondérer les liens de succession entre les événements (ici, chacun des jours) de façon à forcer le redéploiement linéaire de la structure comme on peut le faire aisément sous Gephi:

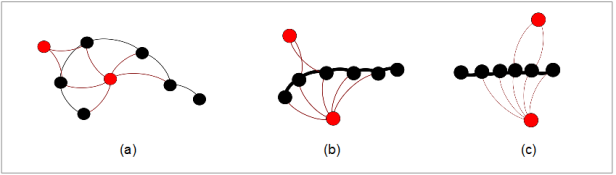
En jouant sur la distribution de la force dans l’univers, de la plus faible (a) à la plus contrainte (c) avec des forces importantes appliquées aux liens de consécution entre événements, on peut donc envisager de produire une déformation significative du squelette du vecteur temporel, synonyme en matière d’analyses des traces sociales d’un parcours ou d’une trajectoire individuelle dans un réseau de connexions collectives.

2. Squelette dynamique de l’espace personnel d’interaction

Les 1062 nœuds (nœuds de chacun des SMS regroupés par jour de l’année + nœuds des correspondants) et 5254 liens du premier jeu de données apparaissent sous un jour nouveau quand on applique une force pondérée aux seuls liens de consécution entre les événements (5000 sous Gephi avec le ForceAtlas2):

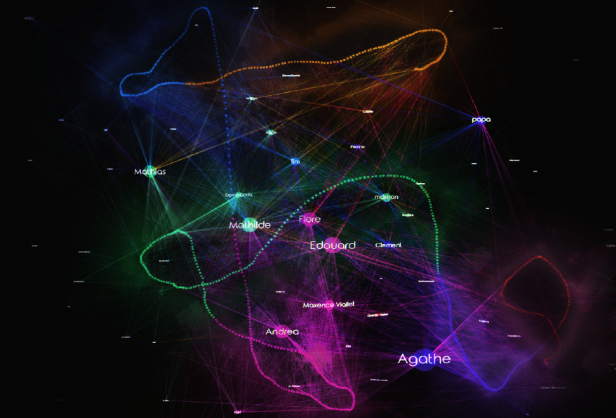
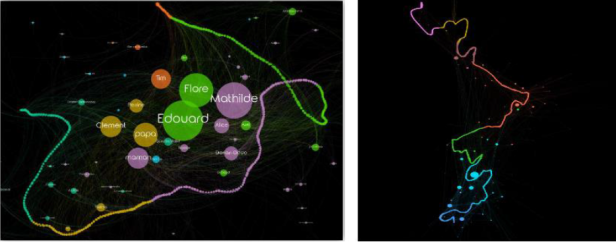
La succession de toutes les connexions liées à l’activité sociale de l’étudiant via ses SMS apparaît sous la forme d’un squelette temporel cheminant dans un espace d’interaction où se retrouvent simultanément positionnés ses contacts. Dans cette spatialisation, plus les contacts sont nombreux avec un acteur, plus le nœud et le label apparaissent au premier plan (sachant que cette métrique quantitative est calculée sur l’ensemble du jeu de données). Ainsi Agathe, Mathilde, Mathias, Edouard ou papa sont ont constitué des interlocuteurs récurrents pour l’étudiant et, avec la méthode testée, ils apparaissent sous la forme de noeuds qui ressemblent à des sortes d’attracteurs sociaux. A partir de la distribution du jeu de force, les circonvolutions du squelette semblent indiquer que durant plus de deux années, des flux de contacts parfois intenses et parfois plus faibles avec certains acteurs centraux dessinent des trajectoires de rapprochement ou d’éloignement et des changements d’orientation de la courbe.

L’intérêt de la méthode réside dans l’effet de concentration de milliers d’informations sous la forme d’une courbe dynamique. Ainsi, ce n’est pas tant l’étudiant lui-même qui est traité sous la forme d’une entité symbolisée par un nœud du graphe (comme les autres acteurs du réseau social) mais le déploiement spatial de l’ensemble des connexions qu’il a produites, ordonnées temporellement et positionnées relativement à l’ensemble de l’espace d’interaction. Le procédé permet donc de transformer les instants ou les événements (ici, calculés en jours) en positions dans l’espace relatif d’interaction. La conjonction ainsi opérée entre temporalité et position dans l’espace incite à passer du « sujet » ou de « l’acteur » aux traces matérielles produites par ses interactions sous la forme technique d’un squelette alors synonyme de trajectoire communicationnelle. Ce que montre l’analyse des données d’usage, c’est que le « sujet » de l’observation est d’abord là où il interagit.

Une seconde expérimentation a été menée sur les données extraites du compte facebook d’un autre étudiant (messages privés via messenger) sur plusieurs semestres d’études. La procédure de traitement du corpus est la même: le graphe comporte 1697 nœuds (en comprenant le squelette temporel) et 5767 liens. La force appliquée aux liens du squelette a été doublée (10.000 ici avec les ForceAtlas2) avec un nombre un peu plus important de liens et de nœuds mais une distribution plus hiérarchisée autour de quelques acteurs centraux. Les deux aspects semblent en partie dépendants: le sujet produisant de nombreuses interactions avec un nombre réduit d’interlocuteurs sur plus de deux années, la structure est naturellement dense et repliée sur elle-même et le squelette temporel mérite donc d’être déployé avec plus de force:

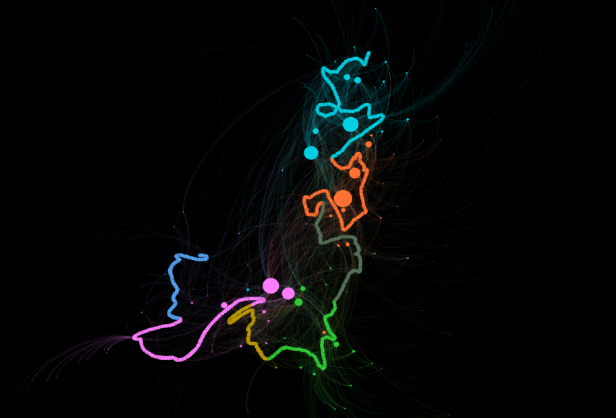
Ici, la trajectoire dessinée par les messages facebook correspond sur plusieurs points évidents avec le premier graphe : quelques grands « attracteurs » sociaux émergent et semblent « attirer » la courbe en raison de la densité des communications sur certaines périodes. A certaines dates (notamment les deux premiers semestres de l’étudiant), les communications semblent se concentrer sur deux interlocuteurs (en bleu en haut du graphe) puis sur deux autres en orange. En revanche, les deux principaux nœuds roses semblent représenter des contacts intenses sur plusieurs périodes. La distribution des couleurs, là aussi, est réalisée avec l’algorithme Modularity sous Gephi. Comme dans le premier cas, les classes de couleurs (ici 7, 6 dans le premier graphe) correspond aux différents semestres et périodes de stage suivis par l’étudiant. A noter que pour les deux sets de données, les informations utilisées pour construire le graphe des connexions commence depuis le jour de la première utilisation d’un smartphone et se poursuit toujours aujourd’hui.

3. Squelette dynamique des espaces collectifs d’interaction

Un autre aspect de la méthode concerne la construction de multi-squelettes, autrement dit plusieurs courbes construites simultanément mais sur la base de liens directs entre les différents squelettes. Si Damien et Félix se sont échangés un ou plusieurs messages, leurs « 2 juillet » seront reliés ensemble dans le graphe. Il s’agit d’éprouver, en quelques sortes, les force d’éloignement et d’attraction, distribués dans le temps, entre ou plusieurs acteurs sélectionnés au préalable.

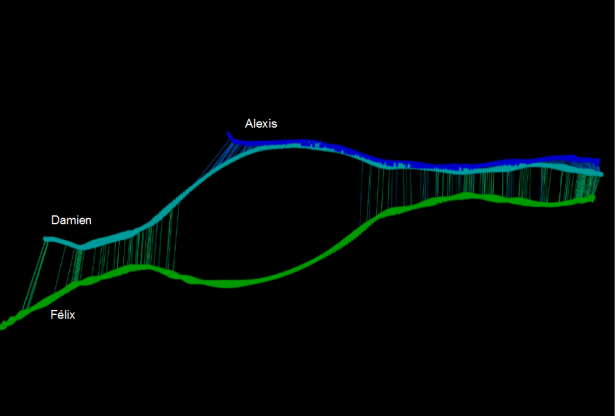
Le graphe comprend 1739 nœuds (les 3 squelettes temporels avec une métrique de type un jour=un nœud) et 2 230 messages. Il ressemble dans son principe aux exemples que donne souvent E.Tufte en matière de synthèse graphique et de visualisation de l’information avec son positionnement de gauche à droite et des courbes qui se suivent de façon (presque) linéaire. Cette « simplicité » graphique est en grande partie due à la méthode de construction du corpus: n’ont été retenus que les messages entre les 3 interlocuteurs et non l’ensemble de leurs communications privés sur la période (ce qui aurait produit des cheminements plus complexes dans le jeu d’attraction-répulsion des trois squelettes). Cette vue réduite à trois acteurs seulement permet de comprendre rapidement comment les squelettes temporels de Damien, Félix et Alexis évoluent au cours du temps: Damien et Félix se connaissaient et échangeaient quelques messages (à gauche) puis ont arrêté (centre). On voit ensuite que Damien rencontre Alexis et qu’en très peu de temps ils se rapprochent beaucoup. Enfin Félix, Damien et Alexis se rapprochent avec la période actuelle intense en échange entre les trois étudiants.

4. Squelettes d’événements récurrents

Certains sets de données recèlent naturellement des squelettes temporels, comme par exemple les données accumulées sur les serveurs qui agrègent les informations liées à des événements récurrents ou cycliques comme des anniversaires, des fêtes annuelles, des concours réguliers ou des événements comme les jeux olympiques ou les coupes du monde de football. Il est donc possible de visualiser de telles chaînes régulières d’événements via une autre dimension de l’information, par exemple les noms des participants à au moins deux des événements. Dans le cas de Ludum Dare, on peut décliner sous Gephi l’ensemble des éditions quadri-mensuelles du concours de création de jeux vidéo en 72h et les relier dans un graphe bi-partite aux multiples joueurs qui ont participé aux éditions:

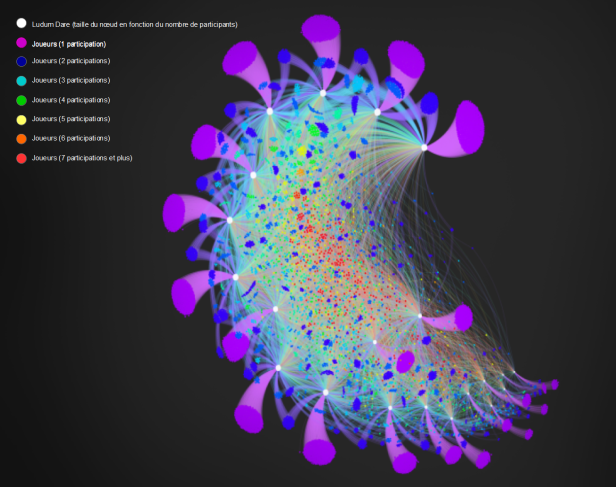
Le graphe bi-partite (session Ludum Dare + tous les joueurs y ayant participé) comporte 15 501 nœuds et 32 352 liens. Les noeuds blancs symbolisent les Ludum Dare tandis que les autres sont les participants. Chaque participant est relié aux Ludum Dare auquel il a participé. La taille des noeuds blanc correspond au nombre de participants de ce Ludum Dare. La couleur des noeuds des participants correspond au nombre de participations. Le violet indique une participation, le bleu foncé, deux participations et ainsi de suite jusqu’au rouge qui correspond à dix participations ou plus. La forme globale que prend le squelette (recroquevillé sur lui-même) indique la présence d’un «cœur» de participants à plusieurs éditions, voire à toutes les éditions du Ludum Dare, tandis que les nœuds des joueurs reliés uniquement à une seule édition tendent à «ouvrir» le pattern avec le ForceAtlas2 utilisé.

De tels graphes bi-partites (événements récurrents + participants) peuvent être produits à partir de nombreux datasets aujourd’hui disponibles. Les Jeux Olympiques, par exemple, représentent ce genre d’événements récurrents qui recèlent d’eux-mêmes cette régularité temporelle qui font visuellement office de squelette: si l’on considère les données  de l’ensemble des Jeux depuis leur création à la fin du XIXe siècle en 1896, le pattern obtenu avec le forceatlas2 apparaît beaucoup plus rectiligne que le premier:

On doit cette rectitude à deux caractéristiques du set de données pris en compte: le fait de prendre en compte seulement les athlètes ayant participé à au moins deux J.O. et  à la longévité historique de l’épreuve. A ce titre, avec ses 31 536 nœuds (essentiellement des athlètes) et 78 223 liens de co-participation aux épreuves (parfois trois J.O. ou plus), le pattern général concentre quelques-unes des caractéristiques majeures des J.O. du point de vue historique: leur absence en 1940 et 1944 ou bien encore l’apparition des J.O. d’hiver dans les données, expliquant la bifurcation du squelette. L’application du procédé des squelettes de façon automatique à des bases de données contenant des indicateurs temporels pourrait constituer un instrument pertinent d’observation des data, dans le domaine de la fouille de données et au-delà.

5. Variations et perspectives

Les pistes de réflexion et d’expérimentation ouvertes par le principe des squelettes de données temporelles sont nombreuses. Quelques-unes, parmi les plus importantes, font désormais partie d’un programme de recherche technologique en data sciences et sont en cours de développement. La première d’entre elle concerne l’étude des propriétés géométriques et statistiques des courbes produites à partir du principe des squelettes: il s’agit de dégager une métrique propre à rendre compte des formes et des changements de direction de la trajectoire. De nombreux paramètres doivent être pris en compte, depuis la structure de données jusqu’aux réglages possible avec un algorithme de type forceatlas2 en passant les jeux de force appliqués aux liens du graphe ou à certains d’entre eux.

Le terrain de l’analyse des comportements humains à partir de l’étude de données réseau constitue à l’évidence un espace prometteur d’expérimentation. En liaison avec les aspects statistiques de la courbe calculée, la notion de trajectoire individuelle et/ou collective devra continuer à être interrogée dans le cadre des patterns d’interaction produits par la méthode. Il s’agit en premier lieu d’interroger les variations de la «topologie sociale»: quel(s) type(s) de trajectoire produisent des univers dans lesquels un acteur échange au cours du temps seulement avec quelques interlocuteurs ou, à l’inverse, avec des interlocuteurs souvent, ou même radicalement différents à chaque communication? Quelle sorte de «grammaire visuelle», avec ses cas limite et exemplaires, pourrait être produite en tenant compte de variable comme l’intensité (ratios possibles entre nombre de connexions et nombre d’interlocuteurs) ou la distribution élargie (quelles sont les trajectoires de tous les acteurs du corpus)? Les phénomènes possibles de concentration de plusieurs trajectoires dans un graphe peuvent-ils être comparés à la notion «d’agrégats communautaires» tel qu’on peut l’entendre dans la communauté du social data mining?  Et puis, comment calculer des métriques d’attraction et/ou de répulsion dans un graphe temps-réel, massivement multi-squelettes, éventuellement multi-sources et selon quel(s) type(s) de segmentation du temps?

Ces questions, comme bien d’autres, pourront être éclairées via des instruments dédiés de recueil et de traitement de données, principe-clé d’une démarche de recherche technologique orientée analyse de données. C’est ainsi qu’a débuté le développement d’un outil automatisé de visualisation de données sous la forme de graphes dotés d’un squelette temporel. Le système de traitement sera accessible via un navigateur et intègrera différents fonctionnalités comme l’homogénéisation du format des données d’entrée de manière prédéfinie (données issues de facebook, SMS…), la création paramétrable des squelettes en fonction de la granularité et de la force des relations entre les éléments du squelette et le développement d’un nouvel algorithme force directed de type forceatlas2. Parallèlement, les contours d’une webapp ont été définis pour produire une sorte de « graphe de la vie » accessible aux usagers de l’application, en particulier suite au vif succès rencontré par les premières visualisations auprès des étudiants de l’U.T.C.

Version PDF

Damien Delmas, Félix Alié, Alexis Schad, Franck Ghitalla

Université de Technologie de Compiègne, juin 2016.

 

Networks

[1] S. H. Strogatz, Exploring complex networks, Nature 410 (6825), 2001.

[2] M. Newman, The structure and function of complex networks, SIAM review 45, 2003.

[3] R. Pastor-Satorras, A. Vespignani, Evolution and Structure of the Internet: a statistical physics approach, Cambridge University Press, Cambridge, 2004.

[4] M. E. J. Newman, M. Girvan, Finding and evaluating community structure in networks, Phys. Rev. E 69, 2004.

[5] A. Vespignani, Complex networks: The fragility of interdependency, Nature 464 (7291), 984–985, 2010.

[6] M. E. J. Newman, Networks: An Introduction, Oxford University Press, New York, 2010.

[7] A.-L. Barabasi, N. Gulbahce, J. Loscalzo, Network medicine: a network-based approach to human disease, Nat. Rev. Genet. 12, 56–68, 2011.

[8] S. Boccalettia, G. Bianconic, R. Criadod, C.I. del Geniof, J. Gómez-Gardeñesi, M. Romanced, Sendiña-Nadalj, Z. Wangk, M. Zaninm: The structure and dynamics of multilayer networks, Physics Reports, 2014.

[9] A.-L. Barabasi, Linked, The new science of networks, Perseus Publishing, 2002.

[10] D. Watts, Six Degrees, the science of a connected age, Norton, 2004.

[11] F. Ghitalla, Méthode et instruments, chapitre 5, Chroniques du Web, Expéditions scientifiques dans l’univers des données numériques et des réseaux, https://ateliercartographie.wordpress.com/2016/04/12/chapitre-5-methode-et-instruments/, 2016.

[12] F. Ghitalla, Des data ciselées, chapitre 6, Chroniques du Web, Expéditions scientifiques dans l’univers des données numériques et des réseaux, https://ateliercartographie.wordpress.com/wp-content/uploads/2016/04/chapitre-6.pdf, 2016.

 

Visualization

[13] C. Ware Information Visualization, Third Edition: Perception for Design (Interactive Technologies) 3rd Edition, 2013.

[14] T. Munzner, Visualization Analysis and Design, Har/Psc Edition, 2014.

[15] E.R. Tufte, The Visual Display of Quantitative Information, 2nd Edition, 2001.

[16] S.K. Card, J. Mackinlay, B. Shneiderman, Readings in Information Visualization: Using Vision to Think (Interactive Technologies), 1999.

[17] Mathieu Jacomy , Tommaso Venturini, Sebastien Heymann, Mathieu Bastian, ForceAtlas2, a Continuous Graph Layout Algorithm for Handy Network Visualization Designed for the Gephi Software, Plos One, 2014.

[18] Bastian M., Heymann S., Jacomy M. Gephi: an open source software for exploring and manipulating networks, International AAAI Conference on Weblogs and Social Media, 2009.